C&汇编基础-逻辑运算

数据宽度

1. 数学上的数字没有大小限制，可以无限大。但是在计算机中，由于受到硬件的制约，数据都是由长度限制的（我们称为数据宽度），超过最多宽度的数据会被丢弃。

2. 4 位宽度表示，假设计算机只能存储 4 位 2 进制数，分别表示

0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

如下图所示，这个圆是一个 4 位宽度的存储器。

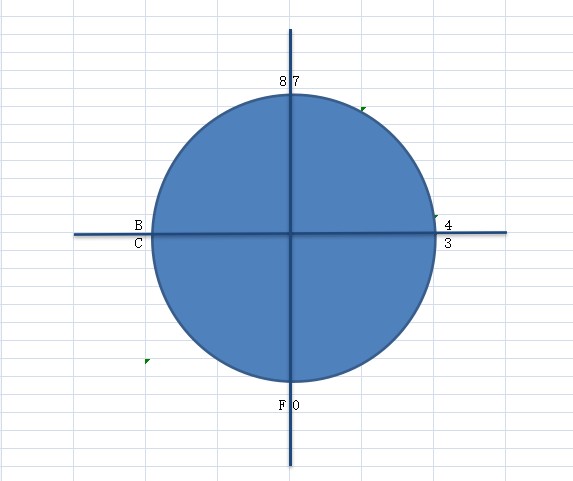
有符号数和无符号数

首先计算机是不会识别正数和负数，它只知道 0 和 1 。正数和负数只是人为的判断这个值是正数还是负数。

无符号数

无符号数就是把存储器的所有空间都用来存正数。例如上面 4 位宽度的存储器，它的无符号数范围就是：0~F

有符号数

有符号数就是把存储器对半分，一半存正数，一半存负数。

就以上面的 4 位存储器为例：你可以理解为把这个 4 位宽度的存储器从中间切成两半，一半存正数、一半存负数。也就是说正数为 07，负数为 8F。

又因为 F 后面的值是 0，所以存储器设计 F 为最大的负数，也就是 F = -1。

4 位存储器的存储规律

正数：

0 1 2 3 4 5 6 7

负数：

-1	-2	-3	-4	-5	-6	-7	-8
F	E	D	C	B	A	9	8

F 是最大的负数，因为从存储器上面看 F+1=10000 。4 位存储器存储不了这么大的值，所以会把最高位 1 丢弃，也就是说值最后变成 0 ：

7	6	5	4	3	2	1	0	-1	-2	-3	-4	-5	-6	-7	-8
7	6	5	4	3	2	1	0	F	E	D	C	B	A	9	8
0111	0110	0101	0100	0011	0010	0001	0000	1111	1110	1101	1100	1011	1010	1001	1000

我们从上面的规律中可以看到，当二进制的最高位为 1 的时候值是负数。

8 位存储器的存储规律

8 位宽度表示，假设计算机只能存储 8 位 2 进制数。

1. 它的无符号数是：0~FF

2. 有符号数是：

正数：0~7F（0~127）

负数：FF~80（-1~-128）

逻辑运算

计算机只认识 0 和 1，那么计算机是如何进行计算的，使得 2(0010)+3(0011)=5(0101)

逻辑或（or，|）

概念：只要有一个为 1 ，值就为 1

    1001010
or  0101001
-------------
    1101011

逻辑与（and，&）

概念：两个都为1时，值为1

    1001010
or  0101001
-------------
    0001000

逻辑异或（xor，^）

概念：两个不一样时，值为1

    1001010
or  0101001
-------------
    1100011

逻辑运算，非（not，!）

概念：1变为0,0变为1

not 1001010
-------------
    0110101

逻辑运算，左移（<<）

概念，数值向左移一位，低位补 0

值向左移一位

    1001010
<<        1
-------------
    0010100

逻辑运算，右移（>>）

概念，数值向右移，高位补 0

值向左移一位

    1001010
>>        1
-------------
    0100101

CPU 运算 2+3 的过程

1. 将两个值进行异或运算，并存储到 R 存储器中

    0010
xor 0011
---------
    0001

R：0001

2. 将两个值进行与运算，然后左移 1 位，并存到 X 存储器中

    0010
and 0011
---------
    0010

    0010
<<     1
---------
    0100

X：0100

左移之后计算机会判断值是不是 0，如果是 0 就取 R 的值，否则就将值存到 X 存储器中，继续运算

3. 将 R 和 X 中的值进行异或，并存储到 R 存储器中

    0001
xor 0100
---------
    0101

R:0101

4. 将两个值进行与运算，然后左移 1 位

    0001
and 0100
---------
    0000

    0000
<<     1
---------
    0000

5. 这里左移后值为 0 ，所以结果取 R 的值，结果为 0101=5

步骤分析

xor：相当于将两个值的位进行相加（除了进位）

and：计算需要进位的值

<<：左移 1 位，实现进位

判断值是否为0：若值为 0 ，说明这个值不需要进位了，前面的 xor 已经算出结果；若值不为0，说明这个值还需要进位，现在还没有算出结果

练习

1. 八进制 2-5 在计算机中的结果是多少？为什么？

8 进制的有符号数是：0~7F、FF~80（-1~-128）

2-5 在 10 进制中是 -3

我们一一对应的找：FF(-1)、FE(-2)、FD(-3)

可以看到我们这里 -3 对应的八进制是 FD

所以八进制的 2-5=FD

2. 使用异或对 87AD6 进行加密再进行解密，加密秘钥是 5

加密

    1000    0111    1010    1101    0110

xor                                 0101
------------------------------------------
    1101    0010    1111    1000    0011
------------------------------------------
    D       2       F       8       3

解密

    1101    0010    1111    1000    0011
xor                                 0101
------------------------------------------
    1000    0111    1010    1101    0110
------------------------------------------
    8       7       A       D       6    

3. 使用逻辑运算计算 2-3=?（涉及内容，逻辑运算、移位，数据宽度）

减法其实就是加法运算：2-3 = 2+(-3)

1. 值相加
    0010
xor 1101
---------
    1111

2. 计算需要进位的值
    0010
&   1101
---------
    0000

3. 进行进位
    0000
<<     1
---------
    0000

4. 值为 0000 ，不需要继续运算，值最后为 1111=F(-1)